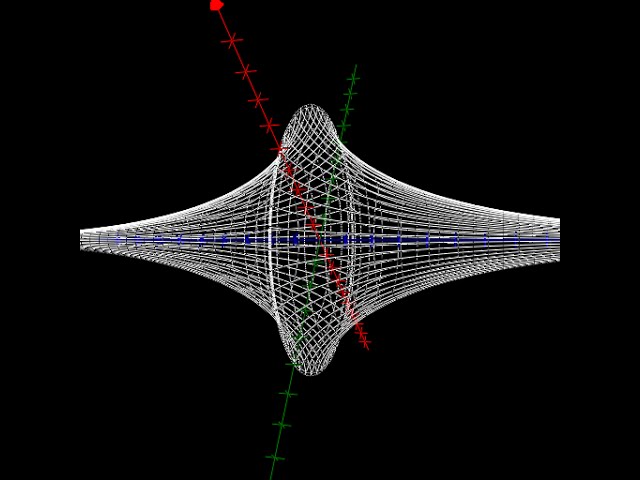
Non-Euclidean geometries
American author and science explorer Clifford A. Pickover explains non-Euclidean geometric systems.
Don’t miss the most important science and health updates!
Subscribe to our newsletter and get the most important news straight to your inbox
Published
July, 2024
Duration of reading
About 1 or 2 minutes
Category
Math
Share

